累積カイ二乗検定(るいせきかいじじょうけんてい、累積カイ二乗法、英:Cumulative chi-squared test)は統計学における仮説検定の一種である。東京大学の竹内啓、広津千尋らによって1966年に田口玄一が導入した累積法を修正して1979年に提案された統計学的仮説検定法である。2つの変数の間、2つの母集団の間に差がないという帰無仮説に対して、対立仮説として帰無仮説の棄却ではなく、一つの変数または両方の変数が増加または減少をする傾向性がある、といった対立仮説を設定する。例えば、薬剤の効果を調べる試験において複数の投与量ごとの反応の程度を見る、といった順序尺度で表される変数について、投与量の水準が増加するにつれて反応が変化する、という対立仮説を立てる。同様の目的のための検定法としてはウィルコクソンの符号順位検定などがある。

帰無仮説

2つの母集団 A, B から抽出して得られる観測値 y {\displaystyle y} により母集団の優劣を比較する場合を考える。各観測値は順序のある k {\displaystyle k} 個の水準のどれかに分けられるものとしたとき、各観測値を y i j   ( i = 1 , 2   j = 1 , 2 , . . . , k ) {\displaystyle y_{ij}\ (i=1,2\ j=1,2,...,k)} で表し、 y i j {\displaystyle y_{ij}} が水準 k {\displaystyle k} に入る確率を p i j   ( i = 1 , 2   j = 1 , 2 , … , k ) {\displaystyle p_{ij}\ (i=1,2\ j=1,2,\ldots ,k)} とする。この場合の帰無仮説は2つの母集団 A, B の間に差がないということを表すため次の式になる

H 0 : p 1 j = p 2 j   ( j = 1 , 2 , … , k ) {\displaystyle H_{0}:p_{1j}=p_{2j}\ (j=1,2,\ldots ,k)}

対立仮説

単に帰無仮説を棄却するのであれば対立仮説は次のようになる

H 1 : p 1 j ≠ p 2 j {\displaystyle H_{1}:p_{1j}\neq p_{2j}}

しかしこの対立仮説ではA, B の優劣を表すことができない。そこで各水準間に順序があることを考えて次の対立仮説を想定する。

H 2 : { ( 1 )   p 11 / p 12 ≥ p 21 / p 22 ≥ … ≥ p 1 k / p 2 k ( 2 )   p 11 / p 12 ≤ p 21 / p 22 ≤ … ≤ p 1 k / p 2 k {\displaystyle H_{2}:{\begin{cases}(1)\ p_{11}/p_{12}\geq p_{21}/p_{22}\geq \ldots \geq p_{1k}/p_{2k}\\(2)\ p_{11}/p_{12}\leq p_{21}/p_{22}\leq \ldots \leq p_{1k}/p_{2k}\end{cases}}} • • • • • • ( 1 ) {\displaystyle (1)} または ( 2 ) {\displaystyle (2)}
H 3 : { ( 1 )   P 1 j ≥ P 2 j ( j = 1 , 2 , … , k − 1 ) ( 2 )   P 1 j ≤ P 2 j ( j = 1 , 2 , … , k − 1 ) {\displaystyle H_{3}:{\begin{cases}(1)\ P_{1j}\geq P_{2j}\quad (j=1,2,\ldots ,k-1)\\(2)\ P_{1j}\leq P_{2j}\quad (j=1,2,\ldots ,k-1)\end{cases}}} • • • • • • • ( 1 ) {\displaystyle (1)} または ( 2 ) {\displaystyle (2)}

ただし P i j {\displaystyle P_{ij}} は累積確率を表す。

P i j = ∑ n = 1 j p i n ( j = 1 , 2 , … , k − 1 ) {\displaystyle P_{ij}=\sum _{n=1}^{j}p_{in}\quad (j=1,2,\ldots ,k-1)}

対立仮説 H 1 {\displaystyle H_{1}} は母集団 A が若い水準(優れているまたはその反対)に分類されることが多いことを表す。 対立仮説 H 3 {\displaystyle H_{3}} はどの累積確率で比較しても同等以上であることを表す。

検定統計量

上記の帰無仮説 H 0 {\displaystyle H_{0}} は次の H 0 j {\displaystyle H_{0j}} が同時に成り立つことと同じである。

H 0 j : P 1 j = P 2 j ( j = 1 , 2 , … , k − 1 ) {\displaystyle H_{0j}:P_{1j}=P_{2j}\quad (j=1,2,\ldots ,k-1)}

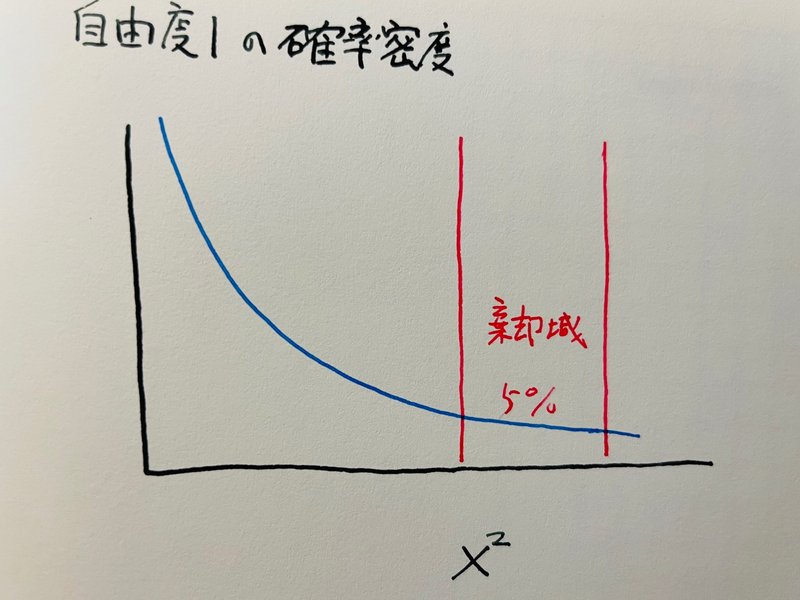
この H 0 {\displaystyle H_{0}} についての自由度 1 のカイ二乗値

χ j 2 = 2 n ( Y 1 j − Y 2 j ) 2 Y ⋅ j ( 2 n − Y ⋅ j ) {\displaystyle {\chi _{j}}^{2}={\frac {2n(Y_{1j}-Y_{2j})^{2}}{Y_{\cdot j}(2n-Y_{\cdot j})}}}
＊ Y i j = ∑ n = 1 j y i n {\displaystyle Y_{ij}=\sum _{n=1}^{j}y_{in}}

この累積するカイ二乗値を結合して一つの検定統計量

χ ∗ 2 = ∑ j = 1 k − 1 χ j 2 {\displaystyle \chi ^{\ast 2}=\sum _{j=1}^{k-1}{\chi _{j}}^{2}}

とする。

適用

傾向のある対立仮説を想定する検定問題で

  • いくつかの二項分布の比較
  • 2つの多項分布の比較
  • いくつかの多項分布の比較
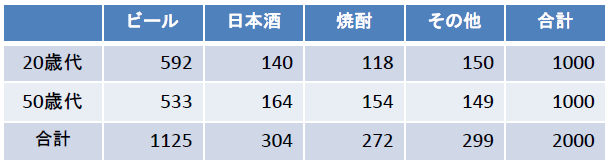
  • 2×k 分割表における独立性の検定

などに用いることができる。

用量反応関係の検定などにおいて累積カイ二乗検定の適用となる分割表のタイプには次のようなものが挙げられる

  • m×2 分割表(順序あり)
  • 2×l 分割表(順序あり)
  • m×l 分割表(列に順序あり)
  • m×l 分割表(行・列とも順序あり)

脚注

関連項目

  • コクラン・アーミテージ傾向検定
  • シャーリー・ウィリアムズ検定
  • ウィルコクソンの符号順位検定
  • クラスカル・ウォリス検定
  • 実験計画法
  • 推計統計学

カイ二乗検定 統計学備忘録 リハビリテーション統計学

カイ二乗検定とは？わかりやすく例を用いて分割表からp値の計算式も簡単に解説！ いちばんやさしい、医療統計

表_24 カイ二乗検定

カイ二乗検定とは何か？｜荒尾 康宏

統計学：χ2乗分布（カイ2乗分布）の意味 森の中